请看题
Given a binary tree, determine if it is height-balanced
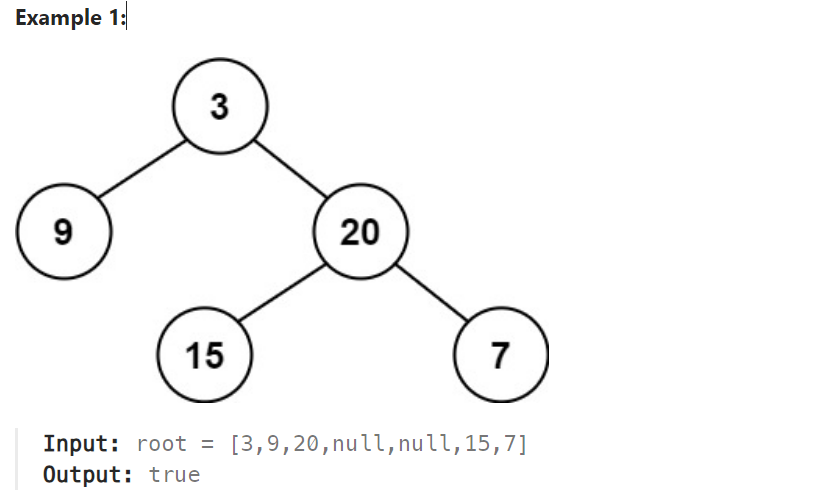
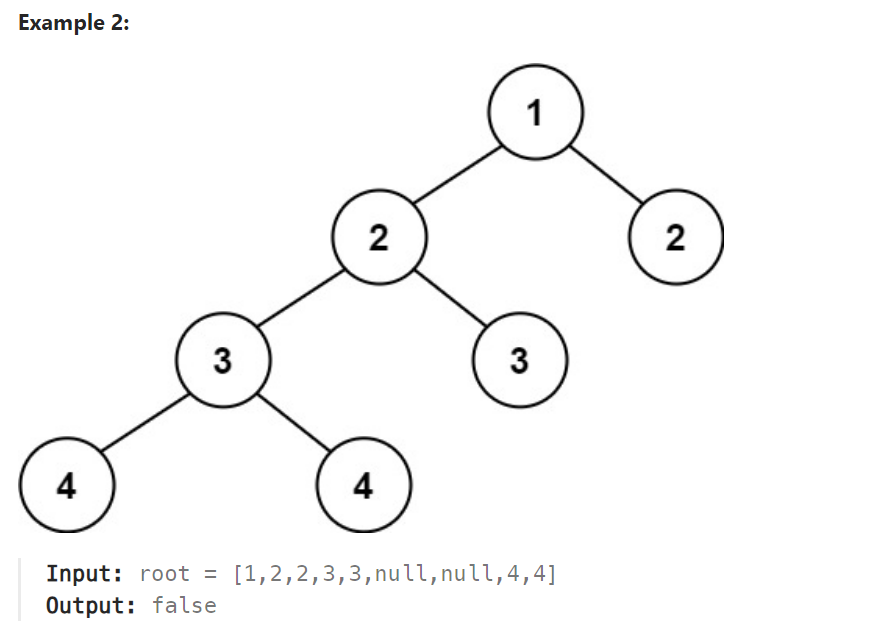

解题思路
在我看来,所有关于二叉树的题目都可以使用递归来解决。那么在这里,在第三个例子中节点为空,那么此树必定为平衡。根据这个条件,我们可以写出如果节点为空直接返回true
1
2
3
4
| if(root == nullptr)
{
return true
}
|
已经解决了第一种情况。接下来看另外几种情况。
如果左节点失衡和如果右节点失衡
这里最大的问题就是怎么去判断节点是否失衡呢?
站在前人的肩膀上,我想到了我可以写一个函数来获取树的高度,请看代码
1
2
3
4
5
6
7
8
| int treeHeight(TreeNode *node)
{
if(node == nullptr)
{
return 0;
}
return 1 + (max(treeHeight(node->left), treeHeight(node->right)));
}
|
treeHeight函数能够为我们获取到树的高度,这里有两个知识点,其一为递归思想,其二为max函数
递归思想
使用递归,可以很好的解决怎么去获取树的高度的问题,一直通过递归调用自身获取左节点或右节点的高度,如果当前的节点为空,那么就说明已经事高度为0或者事高度为上一个节点值。一直重复,直到获取到空值。
max函数
在使用递归的时候,返回的值会有两个,在这里需取最大的那个值来作为我们树的高度
我们已经知道怎么取获取树的高度了,现在就可以来进行第二种判断了
从父节点开始,获取左右节点的各自高度,如果其绝对值超于1,那么为不平衡,返回false
可以写出代码
1
2
3
4
5
| if(abs(leftNode - rightNode) > 1)
{
return false;
}
|
第三种情况
如果左节点的左右不平衡或者右节点的左右不平衡
根据前面我们已经写出的函数,可以进行以下判断
1
2
3
| bool left = isBalanced(root->left);
bool right = isBalanced(root->right);
return left && right;
|
代码
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
| /**
* Definition for a binary tree node.
* struct TreeNode {
* int val;
* TreeNode *left;
* TreeNode *right;
* TreeNode() : val(0), left(nullptr), right(nullptr) {}
* TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
* TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
* };
*/
class Solution {
public:
int height(TreeNode *root)
{
if(root == nullptr)
{
return 0;
}
return 1 + (max(height(root->left), height(root->right)));
}
bool isBalanced(TreeNode* root)
{
if(root == nullptr)
{
return true;
}
int leftNode = height(root->left);
int rightNode = height(root->right);
if(abs(leftNode - rightNode) > 1)
{
return false;
}
bool left = isBalanced(root->left);
bool right = isBalanced(root->right);
return left && right;
}
};
|


