108. Convert Sorted Array to Binary Search Tree

请看题

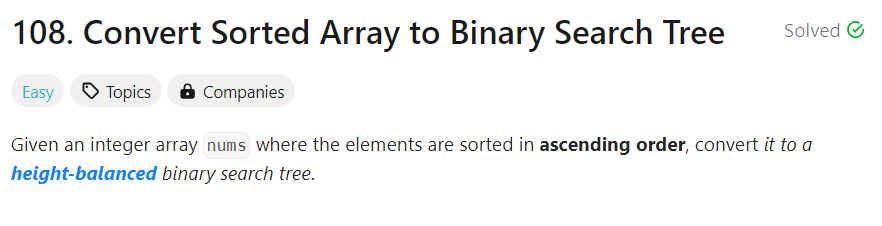
Example

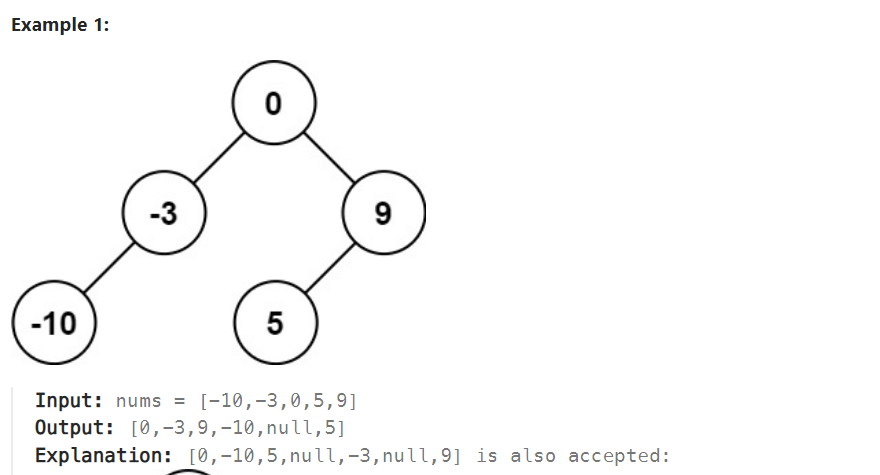
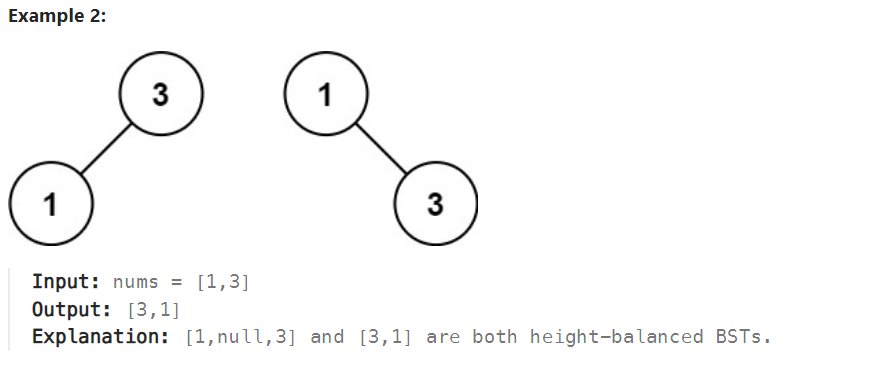
解析

这一道题要求我们进行一个插入操作，插入树的要求为avl树，也就是平衡因子绝对值不能大于1

给定一个排序过后的数组，使用数组来进行插入操作。

最开始的思路

最开始，我想到是我前不久写过的一道题 isBalaced

因为这道题要求我们插入的规则是必须遵守平衡，而isBalanced这道题正好解决了问题，我只需要进行判断，然后插入。

但是真正开始写的时候发现问题了，太太繁琐了，代码太多了。首先，要写两个函数用来判断平衡，其后，要写四个小函数来进行旋转操作，也就是左旋，右旋，左右旋转，右左旋转

代码量多了不说，还极其出错，如有一处错误那么debug时间将会大大的上涨。另外时间复杂度也嘎嘎上升，实属是麻烦之际。

我想了又想，还是找不到解决方法，我决定打开solution查看答案，当我看到答案的时候我惊呆了，原来居然就这么简单！！

先上code

---

Code

/**
 * Definition for a binary tree node.
 * struct TreeNode {
 *     int val;
 *     TreeNode *left;
 *     TreeNode *right;
 *     TreeNode() : val(0), left(nullptr), right(nullptr) {}
 *     TreeNode(int x) : val(x), left(nullptr), right(nullptr) {}
 *     TreeNode(int x, TreeNode *left, TreeNode *right) : val(x), left(left), right(right) {}
 * };
 */
class Solution {
public:
    TreeNode* solution(int start, int end, vector<int> &nums)
    {
        if(start > end)
        {
            return nullptr;
        }
        int mid = start + (end - start) / 2;
        TreeNode *root = new TreeNode(nums[mid]);
        root->left = solution(start, mid - 1, nums);
        root->right = solution(mid + 1, end, nums);
        return root;
        
    }
    TreeNode* sortedArrayToBST(vector<int>& nums) 
    {
        return solution(0, nums.size() - 1, nums);
    }
};

代码解析

首先不去关于返回函数本身，而是去关注我们写的solution函数。此函数接收三个参数，分别是两个int和一个vector。vector是引用

引用等于地址，可进行修改，全局变化，只要引用了

第一个int，表示起点

第二个int，表示结尾

来进入solution函数中的第一个if，如果起点大于终点这说明什么呢？

说明给我们传入的终点为-1，到了这里得要解释一下

在主函数中，调用solution函数，并且传入0， 数组大小-1和数组本身

如果0 > 数组大小-1也就恰好的说明了数组本身size为0，这时候无需插入，因为根本没有元素可以去插入，直接返回nullptr

过了if后，来看一个int变量mid。让我们再来看一看题目

Given an integer array nums where the elements are sorted in ascending order,

elements are sorted 这里直接指出了数组是进行过排序的，那么根据小学的知识我们知道有一个算法叫做二分查找，专门用来给排序过后的数组使用。

这里不多说二分查找，咱们继续下一步。

下一步创建一个root树，并且值为数组的mid，mid也就是前面二分查找的结果。

妙的地方来了！！

因为题目要求我们必须要保持平衡并且要按照二叉树的数据结构来进行构建，这里的mid正好就是完美符合我们要求的一处节点。

头节点必为一个不大不小的值，左孩子必为一个小于头节点的值，右孩子则大于

按照这个方法，不难看见，插入的每处节点都会完美匹配avl树。没有失衡，也就不要去平衡。

最后，返回这颗树，提交答案，过了！！

结论

在没有看见这个仅为天人的答案后，我是绝对想不出来的，这就像数学题，不会就是不会，急了也不会，但是看到答案就是会了，下次再看见也不知道会不会。

再感概一下这个答案是真牛啊

---

结束。